2172. 最大公约数

题意

给定一个数组, 每次操作可以选择数组中任意两个相邻的元素 x , y x, yx,y 并将其中的一个元素替换为 gcd ⁡ ( x , y ) \operatorname{gcd}(x, y)gcd(x,y), 其中 gcd ⁡ ( x , y ) \operatorname{gcd}(x, y)gcd(x,y) 表示 x xx 和 y yy 的最大公约数。请问最少需要多少次操作才能让整个数组只含 1 。
思路

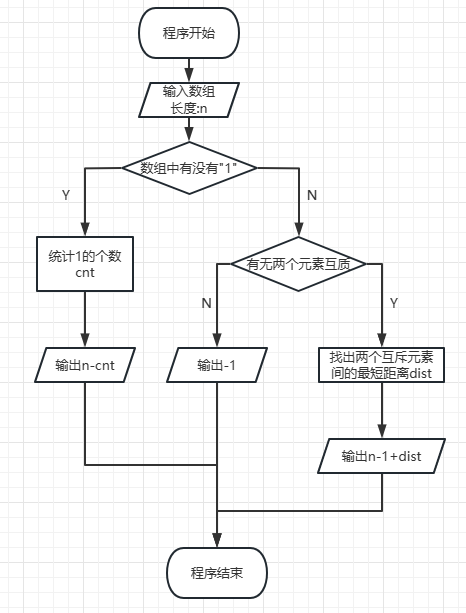
流程图如下

其中两个互质元素的最短距离，可以这么求：
- 首先，目的就是为了让数组中变出一个1，而题目中只让相邻gcd，所以两个互质的不能直接gcd
- 所以我们要进行区间gcd，找到最短长度的区间，使得gcd=1
  - 如abcde，a与e互质，其实相当于a或e中无一个质因子相同，所以也就是a和b进行gcd，然后b肯定会带上a的因子，否则b就是1，然后一直到e
- 可以采用二分或双指针，找最短长度区间
- 可以采用st表或线段树，求区间gcd

代码

'''
Author: NEFU AB-IN
Date: 2023-05-24 12:47:50
FilePath: \LanQiao\2172\2172.py
LastEditTime: 2023-05-24 14:52:22
'''
# import
from sys import setrecursionlimit, stdin, stdout, exit
from collections import Counter, deque
from heapq import heapify, heappop, heappush, nlargest, nsmallest
from bisect import bisect_left, bisect_right
from datetime import datetime, timedelta
from string import ascii_lowercase, ascii_uppercase
from math import log, gcd, sqrt, fabs, ceil, floor


class sa:
    def __init__(self, x, y):
        self.x = x
        self.y = y

    def __lt__(self, a):
        return self.x < a.x


# Final
N = int(1e5 + 10)
M = 20
INF = int(2e9)

# Define
setrecursionlimit(INF)
input = lambda: stdin.readline().rstrip("\r\n")  # Remove when Mutiple data
read = lambda: map(int, input().split())
LTN = lambda x: ord(x.upper()) - 65  # A -> 0
NTL = lambda x: ascii_uppercase[x]  # 0 -> A

# —————————————————————Division line ——————————————————————
a = [0] * N
dp = [[0] * M for _ in range(N)]
Log = [0] * N


def init():
    for j in range(M):
        i = 1
        while i + (1 << j) - 1 <= n:
            if j == 0:
                dp[i][j] = a[i]
            else:
                dp[i][j] = gcd(dp[i][j - 1], dp[i + (1 << (j - 1))][j - 1])
            i += 1
    Log[1] = 0
    for i in range(2, N):
        Log[i] = Log[i >> 1] + 1


def query(l, r):
    k = Log[r - l + 1]
    return gcd(dp[l][k], dp[r - (1 << k) + 1][k])


n, = read()
a[1:] = read()

init()
cnt = sum(i == 1 for i in a)
if cnt > 0:
    print(n - cnt)
    exit(0)

if query(1, n) != 1:
    print(-1)
    exit(0)

ans = INF

for i in range(1, n + 1):
    l, r = i, n
    while l < r:
        mid = (l + r) >> 1
        if query(i, mid) == 1:
            r = mid
        else:
            l = mid + 1
    if query(i, r) == 1:
        ans = min(ans, r - i)

print(ans + n - 1)

2172. 最大公约数

题意

思路

代码