摘要
Title: 893. 集合-Nim游戏
Tag: sg函数、博弈论、有向图游戏的和
Memory Limit: 64 MB
Time Limit: 1000 ms

893. 集合-Nim游戏

题意

给定 n堆石子以及一个由 k个不同正整数构成的数字集合 S
现在有两位玩家轮流操作，每次操作可以从任意一堆石子中拿取石子，每次拿取的石子数量必须包含于集合 S，最后无法进行操作的人视为失败。
问如果两人都采用最优策略，先手是否必胜。
思路

前置知识：
1. Mex运算
  设S表示一个非负整数集合.定义mex(S)为求出不属于集合S的最小非负整数运算
  即: $mes(S)=min{x}$
  例如:S={0,1,2,4},那么mes(S)=3;
2. SG函数
  在有向图游戏中,对于每个节点x,设从x出发共有k条有向边,分别到达节点 $y_1,y_2,····y_k$ ,定义SG(x)的后记节点 $y_1,y_2,····y_k$ 的SG函数值构成的集合在执行mex运算的结果
  即: $SG(x)=mex({SG(y_1),SG(y_2)····SG(y_k)})$
  特别地,整个有向图游戏G的SG函数值被定义为有向图游戏起点s的SG函数值,即 $SG(G)=SG(s)$
3. 有向图游戏的和
  设 $G_1，G_2,····,G_m$ 是m个有向图游戏.定义有向图游戏G,他的行动规则是任选某个有向图游戏 $G_i$ ,并在 $G_i$ 上行动一步.G被称为有向图游戏 $G_1,G_2,·····,G_m$ 的和.
  有向图游戏的和的SG函数值等于它包含的各个子游戏SG函数的异或和
  即: $SG(G)=SG(G_1) \oplus SG(G_2) \oplus ··· \oplus SG(G_m)$
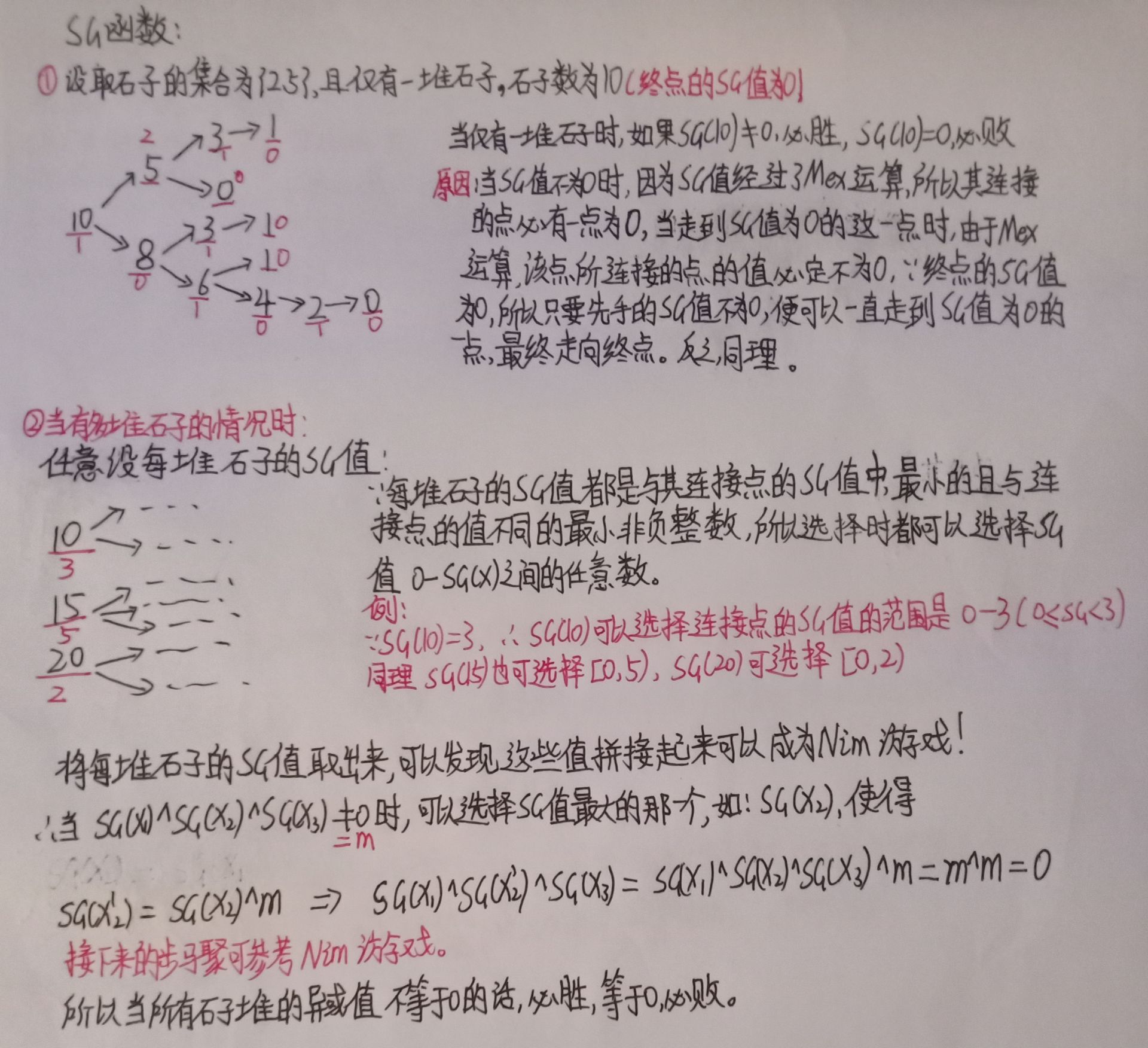
- 那么观察本题中，每堆石子就相当于一场有向图游戏，从最初的石子数，通过集合S的数，连到每个分支，然后从最后面的必输态（也就是sg=0）的状态，反推起点的sg值
  那么n堆石子，就相当于一场有向图游戏的和，就可以应用NIM游戏的结论
- 运用NIM游戏的结论：可以理解为存在一个图的起点的值 $sg_i$ ，可以缩到 $sg_i \oplus x$ （因为是mex函数嘛，对于每个点来说，所有比自己小的点都可以走到，所以一定可以缩到 $sg_i \oplus x$ ）
- 下面是画图的理解
- 为什么记忆化搜索成立？
  因为在本题中，数字集合S不变，则sg函数不变，所以在对某场有向图游戏G，求sg(G)函数时，就可以用记忆化搜索，已经算过的sg值，就不用重复计算了

代码

'''
Author: NEFU AB-IN
Date: 2023-03-21 21:12:31
FilePath: \Acwing\893\893.py
LastEditTime: 2023-03-21 22:02:29
'''
read = lambda: map(int, input().split())
from collections import Counter, deque
from heapq import heappop, heappush
from itertools import permutations

N = int(1e5 + 10)
INF = int(2e9)
f = [-1] * N
# f 代表状态 因为S集合中的数的值最大为10000

def sg(x):
    if f[x] != -1:
        return f[x]

    d = Counter()
    for i in s:
        if x >= i:
            d[sg(x - i)] = 1

    for i in range(INF):
        if d[i] == 0:
            f[x] = i
            return f[x]


k = int(input())
s = list(read())

n = int(input())
h = list(read())

res = 0
for i in h:
    res ^= sg(i)

print("Yes" if res != 0 else "No")

893. 集合-Nim游戏

题意

思路

代码