摘要
Title: 1070. 括号配对
Tag: 区间dp
Memory Limit: 64 MB
Time Limit: 1000 ms

Powered by:NEFU AB-IN

Link

• 题意
• 思路
• 代码

1070. 括号配对

• 题意

  Hecy 又接了个新任务：BE 处理。
  BE 中有一类被称为 GBE。
  以下是 GBE 的定义：
  空表达式是 GBE
  如果表达式 A 是 GBE，则 [A] 与 (A) 都是 GBE
  如果 A 与 B 都是 GBE，那么 AB 是 GBE
  下面给出一个 BE，求至少添加多少字符能使这个 BE 成为 GBE。
  注意：BE 是一个仅由(、)、[、]四种字符中的若干种构成的字符串。

• 思路

  和求最长回文子串类似：AcWing 1222. 密码脱落
  转化：从当前BE变成GBE需要添加最少字符的数量 等价于 当前Be变成最长的GBE需要去掉字符的数量
  那么 至少添加最少字符 等价于 n - 最大GBE子序列的长度

  s变为回文串的最少添加量 = s变为最长回文串的删除量

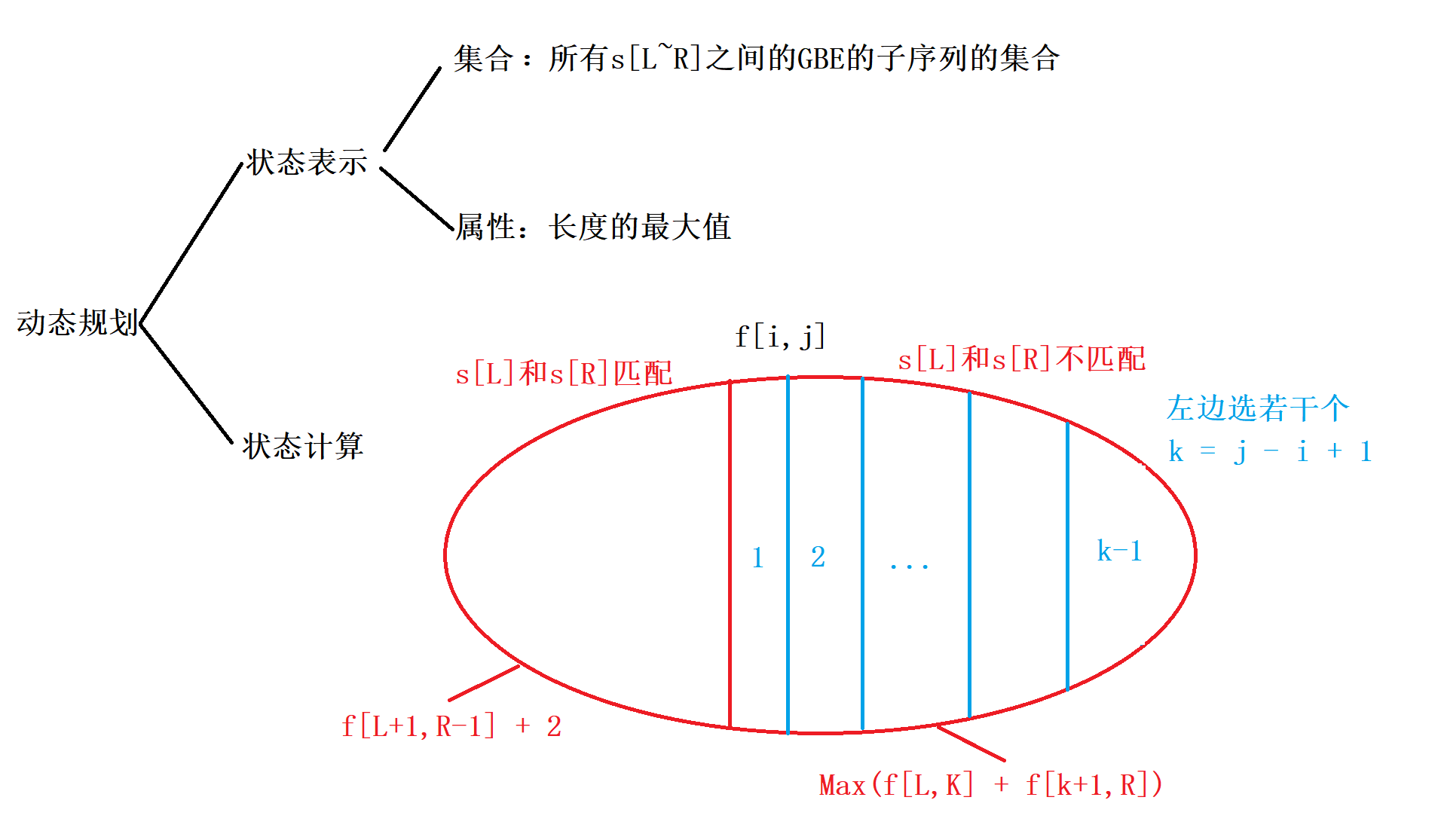
  但由于GBE除了回文还具备别的性质，$()[]$也算GBE，所以当s[i] 与 s[j]不匹配时，应该进一步划分，类似于合并石子，求最大值

  

• 代码

  def judge(a, b):
      if a == '(' and b == ')':
          return 1
      if a == '[' and b == ']':
          return 1
      return 0
  
  
  N = 110
  INF = int(1e18)
  s = " " + input()
  n = len(s) - 1
  
  dp = [[0] * N for _ in range(N)]
  
  for len in range(2, n + 1):
      i, j = 1, len
      while j <= n:
          if judge(s[i], s[j]):
              dp[i][j] = max(dp[i][j], dp[i + 1][j - 1] + 2)
          for k in range(i, j + 1):
              dp[i][j] = max(dp[i][j], dp[i][k] + dp[k + 1][j])
          i += 1
          j += 1
  
  print(n - dp[1][n])