摘要
Title: 1212. 地宫取宝
Tag: 四维dp
Memory Limit: 64 MB
Time Limit: 1000 ms

1212. 地宫取宝

题意

X 国王有一个地宫宝库，是 n×m 个格子的矩阵，每个格子放一件宝贝，每个宝贝贴着价值标签。
地宫的入口在左上角，出口在右下角。
小明被带到地宫的入口，国王要求他只能向右或向下行走。
走过某个格子时，如果那个格子中的宝贝价值比小明手中任意宝贝价值都大，小明就可以拿起它（当然，也可以不拿）。
当小明走到出口时，如果他手中的宝贝恰好是 k 件，则这些宝贝就可以送给小明。
请你帮小明算一算，在给定的局面下，他有多少种不同的行动方案能获得这 k 件宝贝。
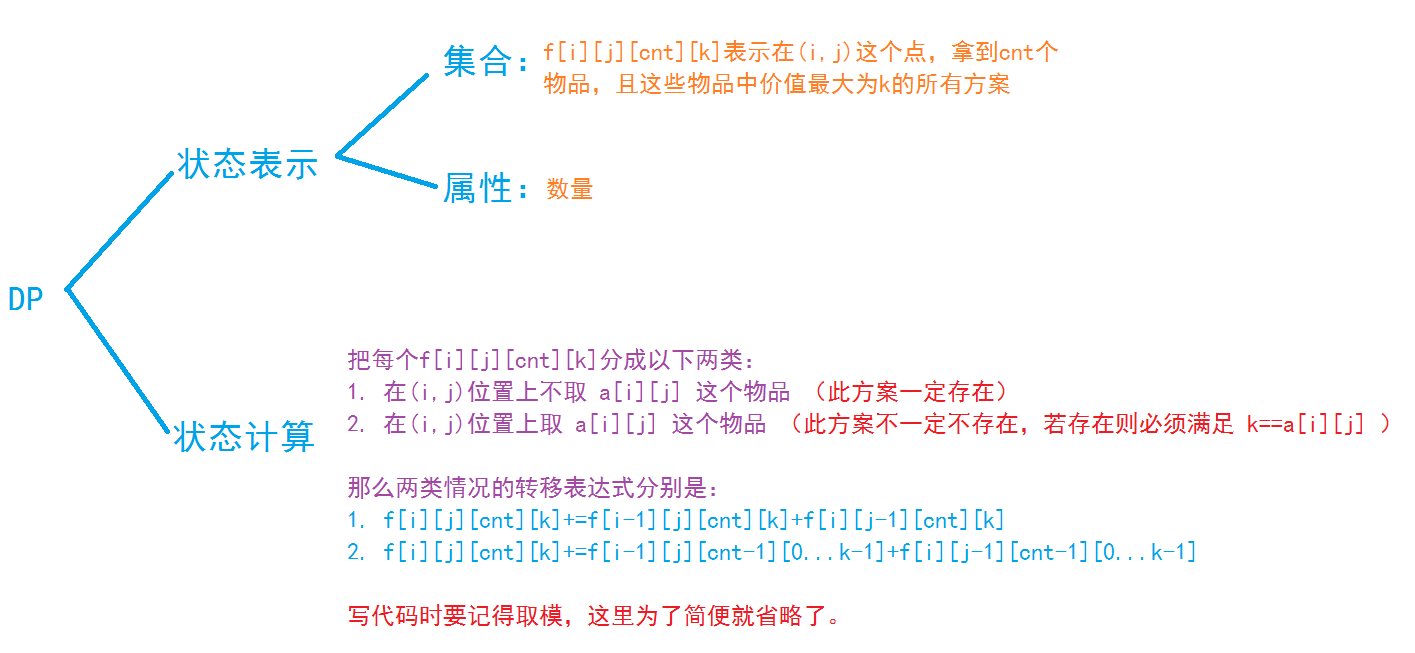
思路

ps:
- 因为题目中说也有价值为0的物品，所以可以让价值整体偏移1, 让q=0成为边界条件
- 如果选了这个物品，那么它一定是目前物品中的最大值

代码

/*
* @Author: NEFU AB-IN
* @Date: 2022-03-23 20:38:59
* @FilePath: \ACM\Acwing\1212.cpp
* @LastEditTime: 2022-03-23 20:58:14
*/
#include <algorithm>
#include <cstring>
#include <iostream>
using namespace std;

const int N = 55, K = 15, C = 15, MOD = 1e9 + 7;

int dp[N][N][K][C];
// dp[i][j][p][q] 表示：在 (i, j) 这个点，拿了 p 个物品，这些物品中价值最大的是 q

int c[N][N];

int main()
{
    int n, m, k;
    cin >> n >> m >> k;
    for (int i = 1; i <= n; ++i)
    {
        for (int j = 1; j <= m; ++j)
        {
            cin >> c[i][j];
            c[i][j] += 1; // 因为题目中说也有价值为0的物品，所以可以让价值整体偏移1
        }
    }
    dp[1][1][0][0] = 1;
    dp[1][1][1][c[1][1]] = 1;

    for (int i = 1; i <= n; ++i)
    {
        for (int j = 1; j <= m; ++j)
        {
            for (int p = 0; p <= k; ++p)
            { //物品
                for (int q = 0; q < C; ++q)
                { //最大值

                    if (p > 0 && q == c[i][j])
                    {
                        for (int s = 0; s < c[i][j]; ++s)
                        {
                            dp[i][j][p][q] = (dp[i][j][p][q] + dp[i - 1][j][p - 1][s]) % MOD;
                            dp[i][j][p][q] = (dp[i][j][p][q] + dp[i][j - 1][p - 1][s]) % MOD;
                        }
                    }
                    dp[i][j][p][q] = (dp[i][j][p][q] + dp[i - 1][j][p][q]) % MOD;
                    dp[i][j][p][q] = (dp[i][j][p][q] + dp[i][j - 1][p][q]) % MOD;
                }
            }
        }
    }
    int ans = 0;
    for (int q = 1; q < C; ++q)
    {
        ans = (ans + dp[n][m][k][q]) % MOD;
    }
    cout << ans << '\n';
    return 0;
}

1212. 地宫取宝

题意

思路

代码