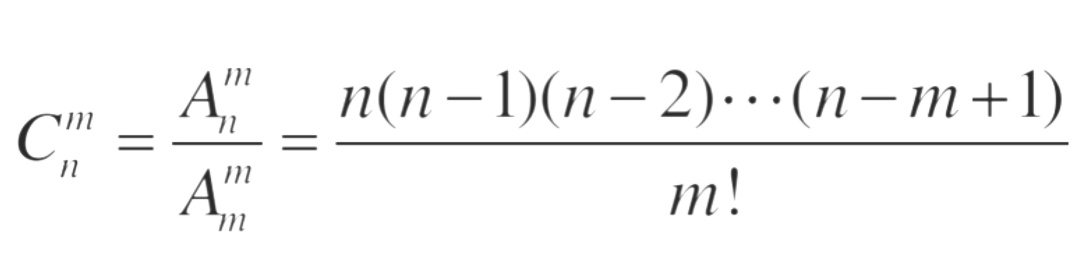摘要
Title: 887. 求组合数 III
Tag: 组合数、Lucas
Memory Limit: 64 MB
Time Limit: 1000 ms

Powered by:NEFU AB-IN

Link

• 题意
• 思路
• 代码

887. 求组合数 III

• 题意

  给定 n 组询问，每组询问给定三个整数 a,b,p，其中 p 是质数，请你输出 C(a, b) mod p 的值。

• 思路

  适合于a, b非常大，模数比较小的情况

  ---

  复杂度$O(log_pN * plogp)$, 其中$plogp$为求组合数的复杂度
  

  Lucas定理：若p是质数，则对于任意整数 1 <= m <= n，有：
  C(n, m) = C(n % p, m % p) * C(n / p, m / p) (mod p)

  ps:

  • n / p 相当于n的p进制数向右移了一位，在公式推导中需要将其移完，所以要递归地求第二项
  • 因为p（模数）是变的，所以不能预处理，需要每次直接求
    • 对应公式
    • 

• 代码

  '''
  Author: NEFU AB-IN
  Date: 2022-03-12 12:04:31
  FilePath: \ACM\Acwing\887.py
  LastEditTime: 2022-03-12 12:04:32
  '''
  N = int(1e5 + 10)
  
  
  def C(a, b): #直接求C
      global p
      i, j, res = a, 1, 1 #i对应的分子，j对应的分母
      while j <= b:
          res = res * i % p
          res = res * pow(j, p - 2, p) % p
          i -= 1
          j += 1
      return res
  
  
  def lucas(a, b):
      if a < p and b < p:
          return C(a, b)
      return C(a % p, b % p) * lucas(a // p, b // p) % p
  
  
  for i in range(int(input())):
      a, b, p = map(int, input().split())
      print(lucas(a, b))