897. 最长公共子序列
摘要
Title: 897. 最长公共子序列
Tag: dp、LCS、dp注意事项
Memory Limit: 64 MB
Time Limit: 1000 ms
Powered by:NEFU AB-IN
897. 最长公共子序列
-
题意
给定两个长度分别为 N 和 M 的字符串 A 和 B,求既是 A 的子序列又是 B 的子序列的字符串长度最长是多少。
-
思路

ps:- 这只是求最大值可以覆盖,求和就不行了
- 自己写状态表示时,i不单单代表i这个点,更多可能是a[1~i]这个区间
- 一般题目问的什么,集合就是什么
- 状态计算,一般看最后一步怎么走,比如
- 背包问题:最后一个物品选择了几个(01背包就是是否选)
- LCS:最后两个元素相等不相等
- LIS:倒数第二个元素选的是哪个
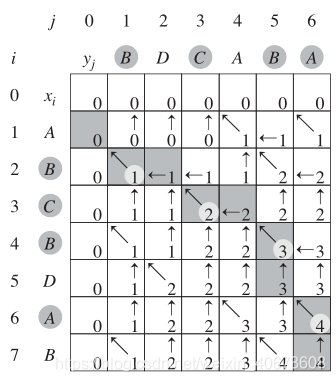
拓展:求串是什么

-
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22'''
Author: NEFU AB-IN
Date: 2022-03-07 16:21:35
FilePath: \ACM\Acwing\897.py
LastEditTime: 2022-03-07 16:21:36
'''
N, M = 1100, 1100
dp = [[0] * M for _ in range(N)]
n, m = map(int, input().split())
a = " " + input()
b = " " + input()
for i in range(1, n + 1):
for j in range(1, m + 1):
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
if a[i] == b[j]:
dp[i][j] = max(dp[i][j], dp[i - 1][j - 1] + 1)
print(dp[n][m])
求串
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47'''
Author: NEFU AB-IN
Date: 2022-04-03 10:00:26
FilePath: \ACM\Acwing\1222.py
LastEditTime: 2022-04-03 10:29:51
'''
N, M = 1100, 1100
dp = [[0] * M for _ in range(N)]
path = [[0] * M for _ in range(N)]
ans = ""
def LCS(i, j):
global ans
if i < 1 or j < 1:
return
if path[i][j] == 1:
ans += a[i]
LCS(i - 1, j - 1)
elif path[i][j] == 2:
LCS(i - 1, j)
else:
LCS(i, j - 1)
n, m = map(int, input().split())
a = " " + input()
b = " " + input()
for i in range(1, n + 1):
for j in range(1, m + 1):
if a[i] == b[j]:
dp[i][j] = dp[i - 1][j - 1] + 1
path[i][j] = 1 #左上
elif dp[i - 1][j] >= dp[i][j - 1]:
dp[i][j] = dp[i - 1][j]
path[i][j] = 2 #上
else:
dp[i][j] = dp[i][j - 1]
path[i][j] = 3 #左
LCS(n, m)
print(ans) #最长公共子序列是什么
print(dp[n][m]) #最长公共子序列长度为多少