摘要
Title: 3. 完全背包问题
Tag: 完全背包、背包问题
Memory Limit: 64 MB
Time Limit: 1000 ms

3. 完全背包问题

题意

有 N 种物品和一个容量是 V 的背包，每种物品都有无限件可用。
第 i 种物品的体积是 vi，价值是 wi。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。
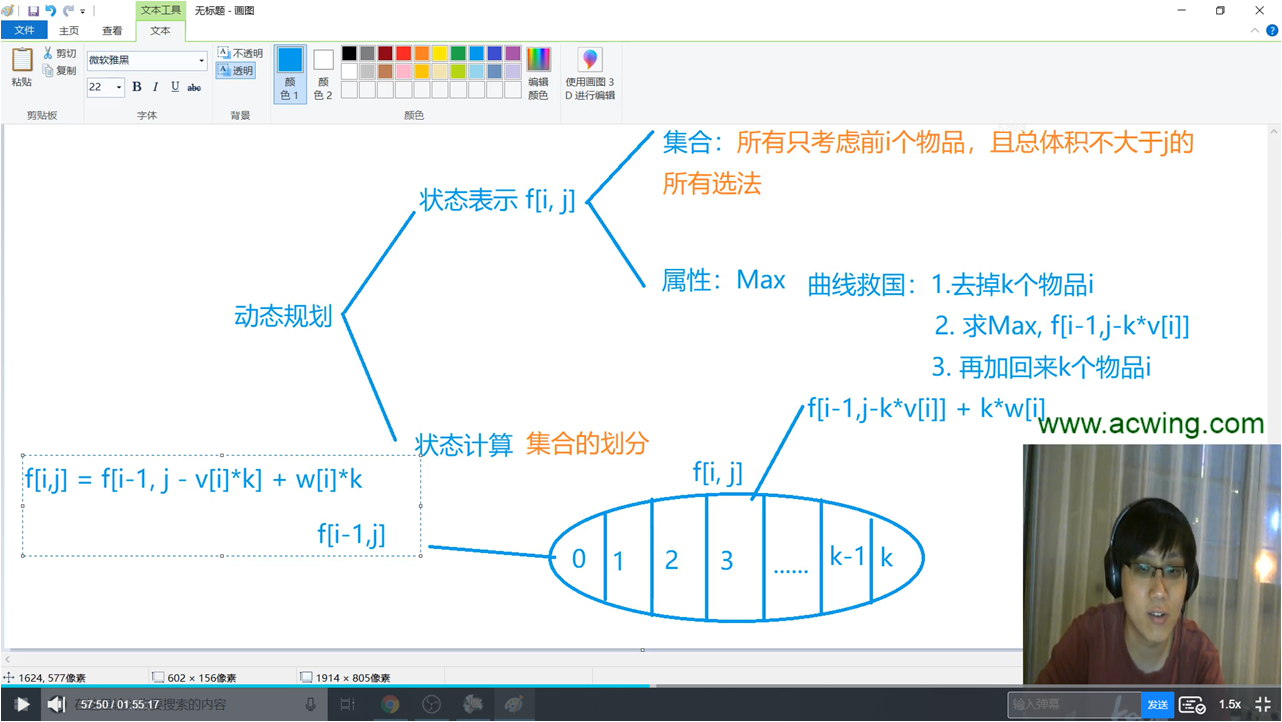
思路

完全背包：每件物品无限用

ps：下面的递推式均是二维，一维的是在代码层面优化的

朴素01背包： $f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i])$
朴素完全背包： $f[i][j] = max(f[i - 1][j - v[i] * k] + w[i] * k)$ $k = 0, 1, 2, ...$
优化后的完全背包： $f[i][j] = max(f[i - 1][j], f[i][j - v[i]] + w[i])$
优化空间的完全背包和01背包： $f[j] = max(f[j], f[j - v[i]] + w[i])$

通俗来说，就是 $f[x][j-v[i]]$ 这一项（第二项）
- 如果 $x = i - 1$ ，那么就是01背包
- 如果 $x = i$ ，那么就是完全背包
所以
- 用的是上一层的状态的话，01背包要从后往前遍历体积
- 用的是这一层的状态的话，完全背包从前往后遍历体积
- 他们的一维递推式是一样的！
背包问题，一般是二重循环
- 第一重循环，枚举的是物品（通常以i代物品的下标）
- 第二重循环，枚举的是体积
- 第三重循环，枚举的是决策（如果是多重背包和分组背包需要）

代码

朴素版本

n, m = map(int, input().split())

N = 1100
v, w = [0] * N, [0] * N
dp = [[0] * N for _ in range(N)]

for i in range(1, n + 1):
    v[i], w[i] = map(int, input().split())

for i in range(1, n + 1):
    for j in range(0, m + 1):
        k = 0
        while k * v[i] <= j:
            dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i] * k] + w[i] * k)
            k += 1

print(dp[n][m])

优化为 $O(n^2)$

n, m = map(int, input().split())
N = 1100
v, w = [0] * N, [0] * N
dp = [[0] * N for _ in range(N)]

for i in range(1, n + 1):
    v[i], w[i] = map(int, input().split())

for i in range(1, n + 1):
    for j in range(0, m + 1):
        dp[i][j] = dp[i - 1][j]
        if j >= v[i]:
            dp[i][j] = max(dp[i][j], dp[i][j - v[i]] + w[i])

print(dp[n][m])

优化为一维

'''
Author: NEFU AB-IN
Date: 2022-03-06 11:29:05
FilePath: \ACM\Acwing\3.py
LastEditTime: 2022-03-06 11:35:40
'''

N = 1010
w, v, dp = [0] * N, [0] * N, [0] * N

n, m = map(int, input().split())
for i in range(n):
    v[i], w[i] = map(int, input().split())

for i in range(n):
    for j in range(v[i], m + 1):
        dp[j] = max(dp[j], dp[j - v[i]] + w[i])

print(dp[m])

3. 完全背包问题

题意

思路

代码